2° FORMA PARA REPRESENTAR UNA ECUACION LINEAL (y=mx + b)

Ecuación de una línea recta

La ecuación GENERAL de una línea recta tiene la forma:

y = mx + b

¿Qué significa?


Gradiente	Intersección Y

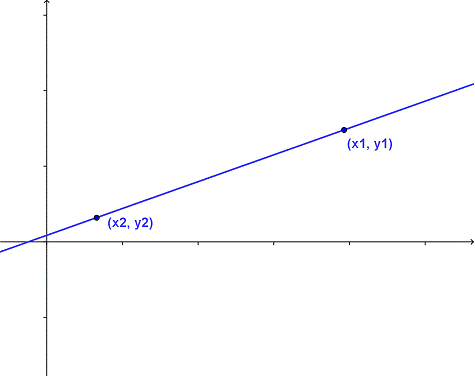
y = cuánto arriba

x = cuán lejos

m = gradiente o pendiente (cuán inclinada es la línea)

b = la intersección Y (donde la línea se cruza con el eje Y)

Sabiendo esto podemos encontrar la ecuación de una línea recta:

Ejemplo 1

b = 1

Por lo tanto

y = 2x + 1

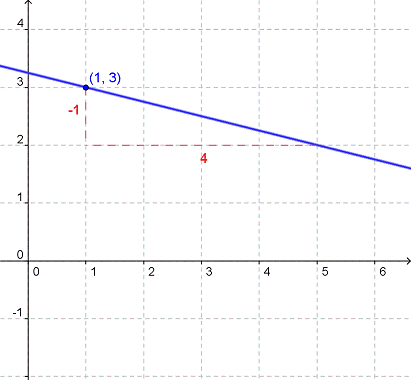
Ejemplo 2

-1

–3

b = 0

Esto nos da y = –3x + 0
¡No nos hace falta poner el cero!

Por lo tanto

y = –3x

ECUACIÓN DE LA RECTA (PUNTO- PENDIENTE)

Las ecuaciones lineales pueden tomar varias formas, como la fórmula punto-pendiente, la fórmula pendiente-intersección, y la forma estándar de una ecuación lineal. Éstas formas permiten a los matemáticos describir la misma recta de distintas maneras..

Esto puede ser confuso, pero en realidad es bastante útil. Considera de cuántas maneras diferentes es posible escribir un pedido de leche en una lista de compras. Puedes pedir leche blanca, leche de vaca, un cuarto de leche, leche descremada, y cada una de éstas frases describiría exactamente el mismo producto. La descripción que uses dependerá de las características que más te importan.

Las ecuaciones que describen rectas pueden ser escogidas de la misma manera — pueden ser escritas y manipuladas con base en las características de la recta que son de interés. Incluso, si una característica es más importante, las ecuaciones lineales pueden convertirse de una forma a otra.

Forma Punto-Pendiente

Un tipo de ecuación lineal es la forma punto-pendiente, la cual nos proporciona la pendiente de una recta y las coordenadas de un punto en ella. La forma punto-pendiente de una ecuación lineal se escribe como. En ésta ecuación, m es la pendiente y (x₁, y₁) son las coordenadas del punto.

Veamos de dónde es que viene ésta fórmula de punto-pendiente. Aquí está la gráfica de una recta genérica con dos puntos trazados en ella.

La pendiente de la recta "aumenta conforme va". Ése es el cambio vertical entre dos puntos (la diferencia entre las coordenadas en y) dividida entre el cambio horizontal sobre el mismo segmento (la diferencia entre las corneadas en x). Esto puede escribirse como . Ésta ecuación es la fórmula de la pendiente.

Ahora digamos que uno de esos puntos es un punto genérico (x, y), lo cual significa que puede ser cualquier punto en la recta, y el otro punto es un punto específico, . Si sustituimos éstas coordenadas en la fórmula, obtenemos . Ahora podemos manipular un poco la ecuación al multiplicar ambos lados de la fórmula por . Que se simplifica a .

es el punto-pendiente de la fórmula. Hemos convertido la fórmula de la pendiente en la fórmula punto-pendiente. No lo hicimos sólo por diversión, sino porque la fórmula punto-pendiente es a veces más útil que la fórmula de la pendiente, por ejemplo cuando necesitamos encontrar la ecuación de una recta dados un punto y la pendiente.

Hagamos otro ejemplo. Considera la recta que pasa por el punto (1, 3) y tiene una pendiente de .

Sustituyendo éstos valores en la fórmula punto-pendiente, obtenemos . Que es la ecuación de la recta.

ELEMENTOS DE UNA ECUACIÓN LINEAL

Cada Ecuación Lineal tiene elementos que le son propios:

Una a más variables que se abrevian mediante letras, y que representan cantidades desconocidas;
Todas las variables están elevadas a la primera potencia, y sin multiplicarse entre sí;
Se establece una igualdad. Es decir, se trata de una proposición que indica que una cantidad es igual a otra.

Ejemplos de ecuaciones que son:
	lineales
	no lineales

	x + 3 = 5
	x + y = 2
	x² + y = 3
	x + y + z = 0,5
	x + z² – xz = 9

ABSCISA Y ORDENADA EN EL ORIGEN

Abscisa y ordenada en el origen

En un plano cartesiano, la grafica de toda recta oblicua - recta inclinada con respecto a la horizontal - siempre corta (intercepta) a los ejes coordenados. La siguiente figura muestra la grafica de una recta L, la misma que corta a los ejes coordenados en los puntos A y B.

Nótese que la recta corta al eje horizontal (eje X) en un punto (A) que está a 3 unidades del origen de coordenadas y corta al eje vertical (eje Y) en un punto (B) que está a 2 unidades del origen de coordenadas.
De acuerdo con lo anterior, la abscisa del punto A es 3 y la ordenada del punto B es 2.
El punto A es un punto del eje horizontal por lo que su ordenada es cero. Luego, las coordenadas del punto A, es decir del punto de corte de la recta L con el eje horizontal, están dadas por A(3, 0).
El punto B es un punto del eje vertical por lo que su abscisa es cero. Luego, las coordenadas del punto B, es decir del punto de corte de la recta L con el eje vertical, están dadas por B(0, 2).

Definimos abscisa en el origen como la abscisa del punto de corte de la recta con el eje horizontal. En este caso, la abscisa en el origen de la recta L es x=3.

Definimos ordenada en el origen como la ordenada del punto de corte de la recta con el eje vertical. En este caso, la ordenada en el origen de la recta L es y=2.

Si conocemos la ecuación de la recta, es posible encontrar la abscisa en el origen, la ordenada en el origen y - por lo tanto - las coordenadas de los puntos de corte con los ejes coordenados.

Así por ejemplo, la recta L mostrada tiene por ecuación
L: 2x + 3y - 6 = 0

Para encontrar la abscisa en el origen, reemplazamos y=0 en dicha ecuación:

2x + 3(0) - 6 = 0
2x - 6 = 0
2x = 6
x = 3

Luego: La abscisa en el origen es x = 3
Las coordenadas del punto de corte con el eje horizontal son (3, 0)

Para encontrar la ordenada en el origen, reemplazamos x=0 en dicha ecuación:

2(0) + 3y - 6 = 0
3y - 6 = 0
3y = 6
y = 2

Luego: La ordenada en el origen es y = 2
Las coordenadas del punto de corte con el eje vertical son (0, 2)

Tenga en cuenta que existe una estrecha relación entre la abscisa en el origen y el punto de corte con el eje horizontal, pero no son ni significan lo mismo. Lo mismo decimos de la ordenada en el origen y el punto de corte con el eje vertical.

TABULACION DE UNA RECTA

Tabulación se refiere al hecho de calcular valores parciales para una función y compararlos en una tabla, de ahí el nombre de tabular.

El método general para gráficar cualquier función es el de tabulación. Consiste en dar valores a la variable x y con ellos calcular los correspondientes a la variable y, los cuales se van anotando en una tabla.

Después se localiza en el plano cartesiano cada punto tabulado así y se unen para obtener la forma de la gráfica buscada.

Por ejemplo, para graficar y= −2x-1, dando valores a la x de - 2, - 1, 0, 1, 2 y 3 se construye la siguiente tabla: